The Fibonacci code can be viewed as a self-clocking serial code for data storage or transmission. For storage use on a medium such as a single-track magnetic tape, or for use as a serial data communications code, Fibonacci code (approaching 0.6667 bits per cell) is 33% denser than Manchester Encoding or Phase Encoding (0.5 bits per cell).

When considering serial codes, a "cell" should be interpreted as the shortest time between transitions. Note that Manchester Encoding is used at the lowest (physical) level for Ethernet communications. A change to Fibonacci coding, implemented in hardware, could increase the speed of any Ethernet link by 33%, with no increase in bandwidth on the link.

"Self-clocking" refers to a code which allows clock and data signals to be easily separated from a single signal. In the Fibonacci code, the time between signal transitions is either 1 or 2 cells. Manchester Encoding and Phase Encoding also have this property. Such codes are most useful for storage on media with a large amount of jitter, or poor speed control, such as magnetic tape. On media with accurate speed control, denser codes, such as group codes, can be used. Group codes achieve greater density by allowing a larger number of cells to pass without a transition, and are commonly used on such media as hard disk drives.

Codes like Manchester Encoding and Phase Encoding convey binary information directly, bit by bit. The Fibonacci code is sent in blocks of a pre-determined length, which can then be decoded to yield a binary number. For instance, since a 32-cell long code maps into an integer between 0 and 2,178,308, it can certainly transmit 21 binary bits (0 - 2,097,151), and hence can replace 42-cells that are Phase Encoded (not counting any prefix or suffix required by either code). This actually leaves 81,157 unused Fibonacci codes, that can be ignored, or used for control or other such purposes.

Consider a serial code represented by two voltage levels, V+ and V-. Let's call the length of the shortest time between voltage transitions a "cell". Further, consider a code in which a single cell between transitions represents a "1" element, and two cells between transitions represents a "0" element. Thus, two "1" elements take exactly the same time, two cells, as one "0" element. Note that the time between transitions alone determines whether an element is a "0" or a "1", not voltage level during the cell time. Elements must alternate between V+ and V- to define the code. (Interested readers might like to note an alternative definition).

It turns out that the number of different codes that are exactly N cells long is equal to F_N+1, where F_N represents the N^th Fibonacci number. See a proof of this. You may recall that the Fibonacci series is a series of numbers beginning with F₁ = 1 and F₂ = 1, and in which each following number is obtained by adding the previous two:

Fibonacci Number:	F1	F2	F3	F4	F5	F6	F7	F8	...
Value:	1	1	2	3	5	8	13	21	...

Note that the traditional definition just above can easily be extended by defining F₀ to be zero; the recurrence relationship (each number is the sum of the previous two) is maintained. We will use the notation F₀ (equaling zero) in the rest of this document:

Fibonacci Number:	F0	F1	F2	F3	F4	F5	F6	F7	...
Value:	0	1	1	2	3	5	8	13	...

The next step: individual codewords in a Fibonacci code of length exactly N cells can be assigned numerical values, assigning each codeword a unique value between zero and F_N+1-1. See a description of how to do this .The result is a weighted code, just like decimal or hexadecimal or octal number representation, except with "column" weights which are the Fibonacci numbers instead of powers of the radix (base), and with the additional property that a single "0" code element uses up two columns. Conversion between the Fibonacci code and binary can then be easily done, implemented either in hardware or software.

Assuming the idle value of the code is, say, V-, it obviously must begin with a transition to V+. The remaining elements then alternate, V-, V+, V-, V+, etc. This produces a problem, however at the end of the code. Although the code has been defined such that each codeword contains the same number of cells, some codes have an even number of elements, and some an odd number. As a result, some codewords end up at V-, and others at V+, after the final transition. The latter cannot be allowed to happen, since the line needs to return to its idle value. This problem can be solved by adding another 1-cell element at the end of the code as a suffix, if the code ends up at V+.

Alternatively, if the overall length of the code, including the suffix, must be fixed, then add a 2-cell element if the code ends up at V+. If the code ends up at V-, add 2 single-cell elements. Thus, the suffix will always be the same length, two cells. Serial codes often also need some sort of prefix, to define the first transition, or to properly synchronize the receiver.

The figure below shows the number "12345678" encoded in Fibonacci code, using a 39-cell code, which is sufficiently long to encode numbers between zero and 102,334,156 (F₄₀-1). Thus, a code this length could be used to encode any arbitrary eight decimal digits. The corresponding number range using Phase Encoding requires 27 bits, or 54 cells, and is also shown. No prefix or suffix is shown on either code.

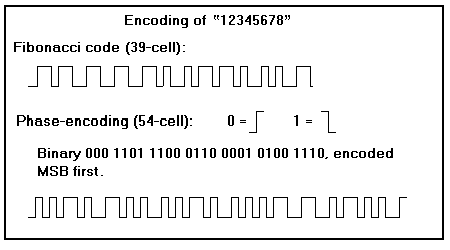
In phase-encoding, one data bit is transmitted by every pair of cells. In the example shown, the data bit is always the second cell of each pair, in which an up-going transition represents a zero, and a down-going transition represents a one. A transition is placed in the first cell of each pair if and only if it is needed to set up the second cell to transition in the proper direction. Thus, there is always a transition in the second, data cell, and only sometimes in the first cell.

Click here to return to Larry Krakauer's home page