

We can use the FN+1 Fibonacci codewords that are exactly N cells long as a numerical code; that is, we can use them to represent integers. Individual codewords in the Fibonacci code can be assigned numerical values, assigning each codeword of length exactly N cells a unique value between zero and FN+1-1. This can be done by treating the codewords as belonging to a weighted code, with each cell "weight" being one of the Fibonacci numbers. The value of a particular Fibonacci codeword is obtained by simply adding together the numerical weights of any cell containing a narrow "1" element, subject to the rules:
It is important to note that the Fibonacci weights are associated with each cell in the codeword, not with each element.
As a sample codeword, consider the code "01011",
of length 7 cells. Then:
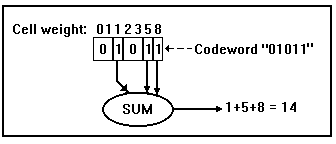
One can prove that, using
this weighting method, an N-cell long code generates exactly the
integers from 0 through FN+1-1; that is, FN+1
distinct integers, with none missing, and no duplicates. This follows
from the method used to generate all
the codes of length N.
The figure above illustrates the simple conversion algorithm
from a Fibonacci Code to its numerical value: simply line up the
code with the Fibonacci cell weights, and add up the Fibonacci
values of each cell containing a "1" (narrow element).
Ignore all pairs of cells containing a "0" (wide element).
The algorithm for conversion from a numerical value to a Fibonacci Code should also be clear now to anyone familiar with radix conversion routines in general. Unlike a binary-to-decimal conversion, though, this is a "mixed-radix" conversion, more like the conversion from days-hours-minutes into total minutes elapsed (60 hours in a minute, 24 hours in a day). With the Fibonacci code, it's best to begin from the Most Significant cell of the code, on the right. Compare the value of the Fibonacci number associated with that cell with the number to be converted. If it's less than or equal, subtract that Fibonacci number from the number to be converted, insert a "1" element (narrow element), move one cell to the left, and iterate.
However, if the value of the Fibonacci number associated with that cell is greater than the number to be converted, insert a "0" element (wide element), move two cells to the left, and iterate. Note: it is very important to move two cells to the left here, to leave room for the wide "0" element. The cell one position to the left cannot be used for a "1" element, even if its Fibonacci number can be subtracted from the residue being converted at that point, because that cell is also occupied by the wide "0" element, so it must be skipped over.
Then just iterate, moving to the left, until you arrive at the left-most cell, and the conversion is complete.
The steps in the conversion of the integer value 14 to a 7-cell Fibonacci code are shown below. The initial "Residue" is set to 14, the number to convert. The conversion starts with "F6" because we have selected a 7-cell long code. If the residue is not zero at the end of the process, the code length selected was not long enough to hold the number. Following the above algorithm:
| Weights | Residue | Test | Action | Code |
|---|---|---|---|---|
| F6=8 | 14 | F6<=14? | Yes, subtract F6, prepend "1" | 1 |
| F5=5 | 6 | F5<=6? | Yes, subtract F5, prepend "1" | 11 |
| F4=3 | 1 | F4<=1? | No, prepend "0" | 011 |
| F3=2 | 1 | Skip | Skip due to "0" in last step | 011 |
| F2=1 | 1 | F2<=1? | Yes, subtract F2, prepend "1" | 1011 |
| F1=1 | 0 | F1<=0? | No, prepend "0" | 01011 |
| F0=0 | 0 | Skip | Skip due to "0" in last step | 01011 |
Note that in most "weighted" numerical
codes, the code representing a given value is the same, except
for leading zeros, regardless of the number of places in the code.
For example, in decimal notation, the two-digit integer "34"
becomes "034" when written with three digits,
"0034" when written with four digits, and so on.
In each case, the final
two digits are the same.
We have chosen to write the Fibonacci
code "backwards", in the sense that the Least Significant
Element is on the left, so in the Fibonacci code, larger codes of
the same value add trailing zeros. The Fibonacci code has
the curious property that the same value is represented by one
code when the overall length of the code in cells
is even, and a different code when
the overall length is odd. Thus, the integer "2" is
represented in odd-cell-length codes by the elements
"111" (or "1110"
or "11100" or "111000", and so on), but in
even-cell-length codes, it's represented by "101" (or
"1010" or "10100" or "101000", etc.).
Note that in the codes just above, the elements of the
code are given, without showing that the "0" element is
twice as wide in cells.
Similarly, suppose we were to convert the number that was converted
just above, 14, into an 8-cell code instead of a 7-cell code.
The result then would have been 01001 instead of 01011. These two codes
have the same number of elements, but the former has one more
cell than the latter, because it has one more zero than before.
The conversion is left as an exercise for the reader (but
remember to start with F7 = 13).
Click here to return to Larry Krakauer's home page
Click here to return to the starting Fibonacci Code page