Consider a code in which a binary "1" is represented by a narrow element, and a binary "0" is represented by a wide element. Call the length of the narrow element a "cell". Further, assume the wide code element, representing binary "0", is exactly twice as long as the narrow code element, so that it is two cells long.

Now: How many different codes can fit in a space exactly "N" cells long? To answer this question, let's start writing them down, remembering that a "0" is two cells long. We will build longer codes from shorter ones by adding on the right.

Clearly, there is only one way of selecting a codeword of zero length (the NUL codeword, with no elements), and there is only one codeword of length 1, which is the codeword "1". For all codes of 2 cells or more, we can construct all the possible codes of any particular length by adding a wide "0" element to all of the codewords that are two cells shorter, and by adding a narrow "1" element to all codewords that are one cell shorter. See the following Figures:

Figure 0: All codes of length 0 cells (none)
Figure 1: All codes of length 1 cell
Figure 2: All codes of length 2 cells
Figure 3: All codes of length 3 cells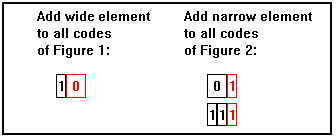
Figure 4: All codes of length 4 cells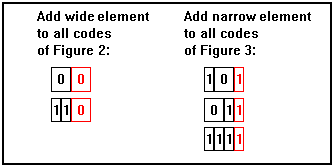
Figure 5: All codes of length 5 cells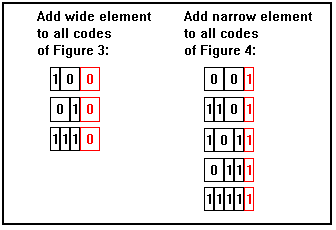

That is, the following two rules have been used: all codes of length N can be constructed by:

Rule A: Append a "0" (which is always two cells wide) to all codes of length N-2 (codes constructed this way are shown in the left column in the Figures)


Rule B: Append a "1" (which is always one cell wide) to all codes of length N-1 (codes constructed this way are shown in the right column in the Figures)

Note that the words "all codes" in the rules include the codes in both columns of the earlier Figures.

Now, back to the initial question: How many codes are there? Note that we can consider that there is exactly one code of zero length, the NUL (or "empty") code, and exactly one code of length 1. For length 2 or greater, following the generation rules above, the number of codes of length N is obviously the sum of the number of codes of length N-1 (rule B) plus the number of codes of length N-2 (rule A). In other words, the lengths form a series of numbers beginning with 1, 1, .... and in which each number is the sum of the previous two:

Length:	0	1	2	3	4	5	6	7	8	...
No. of codes:	1	1	2	3	5	8	13	21	34	...

This, however, is the well-known "Fibonacci" series, named after the greatest European mathematician of the Middle Ages, Leonardo of Pisa, better known as "Fibonacci", "son of Bonaccio." It was first mentioned in his book Liber abaci ("Book of the Abacus"), published in the year 1202. These numbers are traditionally denoted by a subscripted capital "F", as follows:

Fibonacci Number:	F1	F2	F3	F4	F5	F6	F7	F8	...
Value:	1	1	2	3	5	8	13	21	...

And so, the answer is (Tah Dah!):

The number of different codes that are exactly N cells long is equal to F_N+1, where F_N represents the Nth Fibonacci number.

Click here to return to Larry Krakauer's home page