

Viewed as a barcode symbology, the Fibonacci code
conveys almost 60% more information than Code 39 (approaching
0.6667 bits per cell as opposed to 0.42 bits per cell for Code
39), and 40% more information than Interleaved 2 of 5 (0.4745
bits per cell). In making these calculations, the densest versions
of Code 39 and Interleaved 2 of 5 were considered, with a (wide element)
: (narrow element) ratio of 2:1, instead of
the more commonly used 3:1.
Unlike most barcodes, which convey symbols from a
specified set, the Fibonacci code is designed to be converted
to a positive integer. The reader of a Fibonacci barcode must
know what length code to expect; the longer the code, the greater
the upper limit on the integer it can represent. For example,
not counting any start character or stop character, a 20-cell
long code can represent integers between 0 and 10,945 (13.4 bits
of data), and a 44-cell code can represent integers between 0
and about 1.13 X 109 (30.08 bits). A "cell"
is the length of the narrowest element in the barcode.
Thus, the Fibonacci code is a "continuous"
barcode, as opposed to "discrete. That is, it cannot be broken
up into sections such that each section represents a single symbol
from a specified set (or even a pair of symbols, as in
Interleaved 2 of 5). Instead, it transmits a number. Of course,
this number can be interpreted any way the user chooses, so the
barcode can easily be mapped into whatever symbology the user
needs. For instance, since a 20-cell long code maps into an integer
between 0 and 10,945, it can certainly transmit four decimal digits
(0000 - 9999), and hence can replace a four-digit Interleaved
2 of 5 code (28 cells, not counting the start and stop characters).
Consider a barcode in which a narrow bar or
space is called a "1" element, and a wide bar
or space is called a "0" element. Thus, we're using
the term "element" to mean either a bar or a space.
Let's call the width of the narrow bar or space
a "cell". Further, assume the wide code element,
called "0", is exactly twice as wide as the narrow
code element, so that it is two cells wide. Thus, two "1"
elements take up exactly the same space, two cells, as one "0"
element. Note that the width of an element alone determines
whether it is a "0" or a "1" element, not
whether it is a bar or a space (black or white). Elements must
alternate between black and white to define the code. (Interested
readers might like to note an alternative definition).
It turns out that the number of different codes that
are exactly N cells long is equal to FN+1, where FN
represents the Nth Fibonacci number. See a proof
of this. You may recall that the Fibonacci series is
a series of numbers beginning with F1 = 1
and F2 = 1, and in which each following number
is obtained by adding the previous two:
Fibonacci Number: F1
F2 F3
F4 F5
F6 F7
F8 ...
Value: 1
1 2
3 5
8 13
21 ...
Note that the traditional definition just above can
easily be extended by defining F0 to be zero; the recurrence
relationship (each number is the sum of the previous two) is maintained.
We will use the notation F0 (equaling zero) in
these pages:
Fibonacci Number:
F0 F1
F2 F3
F4 F5
F6 F7
F8 ...
Value:
0 1
1 2
3 5
8 13
21 ...
The next step:
individual codewords in a Fibonacci code of length exactly N
cells can be assigned numerical values, assigning each
codeword a unique value between zero and FN+1-1.
See a description of how to do this. The
result is a weighted code, just like decimal or hexadecimal or
octal number representation, except with cell weights
which are the Fibonacci numbers instead of powers of the radix
(base), and with the additional property that a single "0"
code element uses up two cells. Conversion between the Fibonacci
code and binary can then be easily done, implemented either in
hardware or software.
Assuming the barcode is printed with black marks
on a white ground, it obviously must begin with a black mark.
The remaining elements then alternate, white - black - white -
black, etc. This produces a problem, however at the end of the
code. Although the code has been defined such that each codeword
contains the same number of cells, some codes have an even
number of elements, and some an odd number. As a result,
some codewords end on a black element, and some on a white element.
The latter cannot be allowed to happen, since if the final element
of the code is white, there is no way of determining whether it
is narrow or wide, as it never ends (it just trails off into the
paper). This problem can be solved by adding another narrow black
element at the end of the code as a "stop character",
if the code ends with a white element.
Alternatively, if the overall length of the code,
including the stop character, must be fixed, then add a wide black
element if the code ends in a white element. If the code ends
in a black element, add a narrow white element, followed by a
narrow black element. Thus, the "stop character" will
always be the same length, two cells. Note that all barcodes have
start and stop characters. If the Fibonacci barcode is to be read
with a wand, some sort of start character will also be
needed, to allow the reader to determine the wand speed by reading
a few bars of known width.
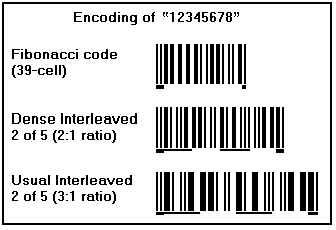
The figure below shows the number "12345678"
encoded in Fibonacci code, and in two different versions of Interleaved
2 of 5: a "dense" version, with a wide:narrow ratio
of 2:1, and the more traditional version, with a wide:narrow ratio
of 3:1. The Fibonacci code uses a 39-cell code, which is sufficiently
long to encode numbers between zero and 102,334,156 (F40-1);
hence, any 8-digit decimal number. The Start Character and Stop
Character have been underlined heavily in each code, with the
Interleaved 2 of 5 Start Character being used for all the codes.
In the Interleaved 2 of 5 codes, alternate pairs of digits have
also been underlined.
Click here to return to Larry Krakauer's home page