
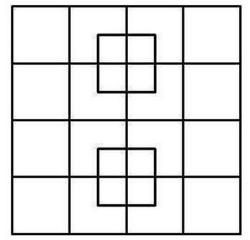
A puzzle has been floating around the Internet, and particularly around Facebook, for a few years now. It asks people to count the total number of squares they see in the figure to the left. Each time the puzzle is posted on Facebook, it seems to attract tens of thousands of replies, most of them wrong. I've replied myself, with a brief explanation of my reasoning. But it's much better to actually show all the squares, which I do below by filling each with red. It appears that a lot of people get lost in the counting. I think it helps to organize the count by looking separately for squares of different sizes. It seems simplest to consider the entire width of the figure given to be four units, so that the squares of the main grid (those largest in number) have sides of 1 unit. Then you can see that the figure holds squares with sides as small as half a unit, and one square of size 4 X 4 (the big outer square). Let's count them starting with the smallest ones, and proceeding to the largest: There are 8 squares whose side is one half a unit:  There are 18 squares whose side is one unit. The first sixteen belong to the grid inside the big square, but there are two more in the two squares superimposed on the grid:  There are 9 squares whose side is two units:  There are 4 squares whose side is three units:  There's 1 square whose side is four units:  Note that although I've highlighted each square by filling it in, I'm defining a "square" as comprising the lines that surround it. I think that was the original intent of the puzzle. In mathematics, the idea of a "line" is an abstract concept - it has length, but no width, for example. A line drawn on a piece of paper is only a representation of the abstract idea of a mathematical line. In those terms, a "square" is the abstract idea of a planar figure surrounded by four lines of equal length, with right-angles in all four corners. Having created the figures above, it occurred to me that there must be thousands of web sites that have done the same. In fact, a search on the phrase [ "how many squares" ] produces nearly two million hits, many of them sites illustrating the answer to the question, as I've done above. One interesting site with an alternative solution is called That stupid "how many squares" puzzle. It gets the answer 47, by including "squares" like this one: 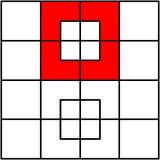 The author considers that to be a square with fat lines around it, as opposed to the thin lines that comprise the grid. As I've said, I don't think that was the intent of the original puzzle. That's not a square in the mathematical sense. There are many other sites that enumerate the squares included in the solution to the puzzle, often using animation to highlight the 40 squares in sequence. Some of these are: There are many, many more - you can do your own search. I like my own diagrams above - you can print them on a few sheets of paper. It's hard to print an animated gif. One moral of the story is that if you want the answer to a question, do an Internet search. The correct answer is probably out there. Although you may also find every possible wrong answer, and every possible alternative interpretation. I wrote this blog entry because I was asked for my solution to the puzzle by both my wife Margie and my niece-in-law Carolyn Campbell. I seem to be the go-to person in my extended family for many questions, particularly of a technical or mathematical nature (see my sister Alice's "guest blog entry" called Ask Larry). But even if I knew everything (and I certainly don't), the Internet has now rendered me obsolete. Just Google it. Here's a much more difficult, but much more interesting problem. If you put n dots on a circle, and connect them with all the possible chords, what's the maximum number of regions the circle can be divided into? Here are the cases for n = 1 through 5: 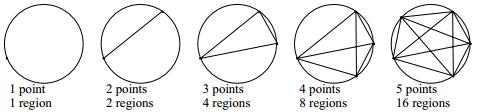 The pattern is clear: 1, 2, 4, 8, 16, ... regions - it must double each time. That would make the formula for the number of regions R = 2(n-1). Except that's not the case. Here it is for six points on the circle. You have to be a bit careful where you put them to get the maximum number of regions. Allowing three of the chords to cross at a single point (shown with a red dot on the left below) is not acceptable. That's because it gives you fewer regions, and the problem statement specifies the maximum number of regions: 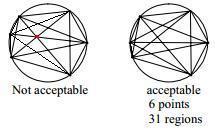 And lo and behold, there are only 31 regions, not 32 (count them!). In fact, the formula for the number of regions as a function of the number of points on the circle "n" is not the simple R = 2(n-1), but rather:   Note 1: This footnote is for the really mathematically inclined. Poking around the internet, I've determined that this formula gives the sum of the first five numbers in successive rows of Pascal's Triangle (or the sum of the entire row, if there are less than five). See below, in which the first five numbers to be summed in each row are highlighted in red:
This means that the formula can be expressed as: 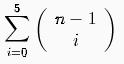 ... subject to the constraint that any term for which i > n is zero. The notation inside the summation, including the parentheses, can be read as "the number of combinations of n-1 things taken i at a time". It generates the well-known binomial coefficients that form Pascal's Triangle. The triangle is easily constructed - note that each number is the sum of the two above it. That's why the sum of all the numbers in any given row is a power of two - because the numbers in each row contain the numbers in the previous row twice. And you can see why the formula yields powers of two up through n = 5, but then starts growing more slowly. Things in mathematics are marvelously interconnected. [return to text]
 |
 Here's an entry for "
Here's an entry for "