This entry discusses the games of chess and nim, and by extension, all finite deterministic games. It gets a bit technical, but even if you only read the first part, you might find it interesting.

1. The game of chess must be one of three things (to be better defined below): a forced win for white, a forced win for black, or a draw (tie).

2. It is not hard to write a computer program which, once started, will definitely run to completion in a finite amount of time, at which point it will type out which of the above three possibilities is the case.

3. But although the question can definitely be answered with a finite amount of computation, we don't know the answer, and probably never will.

Chess, played by tournament rules, is a finite, deterministic game. "Finite" means that all chess games must end. Tournament rules provide for terminating, in a draw, games that might otherwise go on endlessly. "Deterministic" means that there is no chance (randomness) involved in chess, as in, for instance, a game of cards. The list of possible moves at every point in a game of chess is determined by the positions of the pieces on the board, the past history of the game, and nothing else.

By rule in chess, "white" plays first, and "black" second. To say that chess is "a forced win for white" means that if the white player were capable of optimal play, he or she could force a win no matter what moves black makes. Obviously, symmetrically, to say that chess is "a forced win for black" means that if the black player were capable of optimal play, he or she could force a win no matter what moves white makes. To say that chess is "a draw" (or "a drawn game") means that if both white and black were capable of optimal play, the game would end in a draw every time. An example of a drawn game is tic-tac-toe. The only way a player can win at tic-tac-toe is if the other player makes a mistake.

Because chess is deterministic, it's possible to write a computer program to play out every possible game. Because it is a finite game, the computer program will eventually finish its job, and report back on the answer to the question. Finding the answer would be called "solving" chess. The game of checkers has been solved - it's a draw. Why, then don't we know the answer to the same question about chess? After all, we have, some pretty powerful computers.

The answer is the sheer number of possible chess games. It's estimated that there are about 10⁴⁰ possible chess positions, although in most of them, one side is hopelessly lost. Don't like scientific notation? 10⁴⁰ equals

Suppose we could build a computer that could evaluate a million of those chess positions each second. Then it would take 10³⁴ seconds to evaluate all the positions (that is, we've only shaved off six of the 40 zeroes). Evaluating at that rate, it would take over:

to evaluate all the positions, where a "millennium" is a thousand years. In other words, forget it. Not only are the computers of today not up to the job, no computer we can even conceive of comes even close.

And hence the interesting state of affairs posited in the three points at the top of this entry: there is a simple question that can only have one of three simple answers, a computer program can easily be written which, if run to completion (and it will definitely run to completion) will unquestionably give us the answer, and yet we don't know the answer, and probably never will.

Just how could a computer program be written that would "solve" chess? The rest of this entry gets even more technical than the first part, but if you've read this far, I'll bet you can understand it, even if you skim over some of the details. The best way to make something clear is by example, and for that, I'll need a simpler game than chess. Let's see exactly how a computer program could work at "solving" chess by looking at a simpler game called "nim".^{Note 1}

The picture above shows a scene from the enigmatic 1961 Alain Resnais film "L'Année dernière à Marienbad" (variously translated as "Last Year in Marienbad", or "Last Year at Marienbad"). Notice the dominoes on the table laid out (as seen by the man on the right) in four rows of 1, 3, 5, and 7. The players are about to start a game of "1-3-5-7 nim". In nim, players alternate turns, and on each turn, a player can remove any number of tokens from any single row (but the player must remove at least one token). The object of the game is to force your opponent to remove the last token.

Here's a sample game:

To be able to describe the game, I've labeled each position with a letter to the upper-left of the box showing the tokens (shown as red dots). The number to the upper-right of the box shows the player to move, 1 or 2 ("1" being the first player to move). The game proceeds as follows:

        From A, player 1 removes four tokens from the fourth row, → B
        From B, player 2 removes four tokens from the third row, → C
        From C, player 1 removes the entire second row, → D
        From D, player 2 removes two tokens from the fourth row, → E
        From E, player 1 removes one token from the first row, → F
        From F, player 2 removes one token from the third row, → G
        From G, player 1 is forced to take the last token, and hence loses

But even the "Marienbad game" version of nim is too complex for me to use as an example. Since nim in general can be played starting with any number of rows of any number of tokens, let's look at a trivial version of the game, with only two rows of two tokens each. How can we analyze it? (Even if you skim the text below, you can still get the general idea.)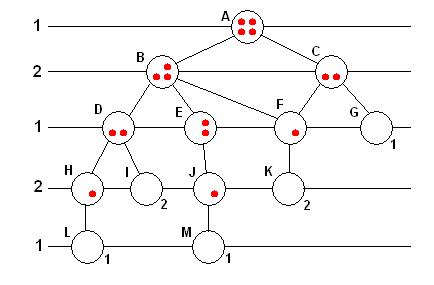

The "move tree" above shows every possible game of 2-2 nim. The board positions are shown in circles, with the circle labeled "A" showing the starting position. Player 1 can only make two initial moves: take one token out of the top row, giving position B, or take the entire top row, giving position C. Player 1 could also take these tokens out of the second of the two rows, but the result be the same, except with the rows interchanged. The diagonal lines going down from position A show the two possible moves for player 1.

The next lower horizontal line in the picture above (with a "2" on the left) shows the possible moves for player 2, which can result in only four different results, shown on the third line as D, E, F, and G. In one of the resulting positions, "G", all the tokens have been removed. It has thus been labeled to the lower-right of the circle with a "1", meaning the game has been won by player 1 (since it was player 2 who removed the last token).

Tracing through the "tree" shows every possible game. All of the final game positions, G, I, K, L, and M have been labeled at the lower-right with the number of the winning player.

Now that we have the entire "game tree", it's possible to work back from the bottom to the top, using what's called a "min-max" procedure (for "minimum-maximum"). Player 1 always wants to choose a move leading to a minimum value, a 1, representing a win for player 1. He only chooses a move leading to a 2 if he is forced to do so. Similarly, player 2 always wants to choose a move leading to a maximum value, a 2, representing a win for player 2, and only chooses a move leading to a 1 if there is no other choice. Working from the bottom up, we can then label every position, as follows: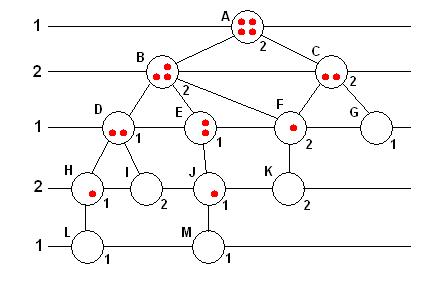

This gives the answer we were looking for. Since the top position, A, ends up getting labeled with a 2, we can conclude that the game of 2-2 nim is a "forced win for the second player". A look at the game tree shows that the second player can always get to position F, immediately winning the game.

By the way, the "Marienbad game", 1-3-5-7 nim, is also a forced win for the second player! That's one way the player in the film always wins - he usually offers, generously, it seems, to let his opponent move first. At one point, an opponent asks to move second, but he loses anyway. Remember, a "forced win for the second player" is only "forced" if the second player plays optimally. If not, he can still lose. ^{Note 2}

Nim has been "solved" in the general case, and there is an optimal strategy for any version of the game (that is, any number of rows with any number of tokens in each). The optimal strategy can be easily computed in your head as you play. It turns out, oddly, to be based on counting the number of tokens in the rows in the binary system! ^{Note 3}

Finally, back to chess. Exactly the same procedure could be used by a computer program to analyze chess: create the "move tree", and then use the "min-max" procedure to ultimately label the initial position. Unlike nim, chess has the possibility of a draw, but that doesn't affect the basic process. You just assign a value of +1 to a win for white, -1 for a win for black, and 0 for a draw. You can then use the same min-max procedure illustrated above, with white trying to maximize the result, and black trying to minimize it.

It's not necessary to have enough computer memory to represent the entire move tree - it can be explored in pieces, and at any given moment, only enough memory is needed to represent the game from the initial position to that point. When the program terminates, as terminate it must, the initial chess board position will have a number, +1, 0, or -1, representing either a forced win for white (the first player to move), a drawn game, or a forced win for black, respectively.

Now if we only had the billions of billions of billions of millennia needed to wait for the answer.
 

Note 1:   Since I'm interested in word origins, this is a good place to observe that the name of this game is thought to be derived from the German verb "nehmen", meaning "to take". In the familiar "du" form, the imperative is "nimm", meaning "Take!"   [return to text]

Note 2:   It might seem odd that it can be an advantage to be the second to play, but that is indeed the case for certain versions of nim (such as 1-3-5-7 nim and 2-2 nim).

If you have followed this entry, you now understand what it means to say that chess must be either a forced win for white, a forced win for black, or a drawn game. Probably only some chess players understand this question, as you now do. If you ask them what they think the answer is likely to be, most would probably guess that chess is a drawn game, but some think that it could be a forced win for white. Most think it highly unlikely that it could be a forced win for black, given the distinct advantage observed for the first mover in tournament play.   [return to text]

Note 3:   You can find many analyses of nim on the web. Click the following link for a good brief history of nim, and the next one for a discussion of the optimal strategy (you'll need to scroll down).

Although nim is generally defined such that the player forced to take the last token loses, it can also be defined such that the player taking the last token wins. Oddly, the winning strategy is the same for both versions, except for a minor difference at the end of the game. The winning strategy essentially keeps a player in control of the game until the point where there is only a single token in every remaining row.   [return to text]