Unfortunately, the bicycle was not one that two people could comfortably ride. We started out walking together, with me pushing the bicycle, but then I had a better idea - a way we could get there faster, while still arriving at the same time. We could do that if we each bicycled half way, and walked half way.
So Diane set off, carrying the bicycle lock, but leaving me the key. I proceeded to walk to the agreed upon corner, and as I arrived there, I was pleased to see the bicycle, chained to a pole. My brilliant idea was working! But just as I unlocked the bicycle, who should step out of a nearby doorway but Diane. I looked at the sign above the door - it was a patisserie (a pastry shop). In one hand, Diane held an éclair. It seemed that upon arriving at the designated corner, Diane had noticed the patisserie, and had found it irresistible. So there we were, now half way to the Place Clemenceau, together again. Since the past is past, I guess the logical thing to do would have been to have picked another location halfway from our new starting point. But I recall being so annoyed at Diane for ruining my wonderful idea that I got on the bicycle and rode off, making her walk the rest of the way (as we had originally planned). Let me add that Diane was not alone in being magnetically drawn to Pau's patisseries. All the girls in our group seemed to spend a lot of their time in these French gardens of Eden (for some reason, the girls much more than the boys). Once, during a morning French lesson, the professor decided to expand our vocabularies by asking the students to name a few French pastries. Overwhelmed by the response, he called a halt to the exercise after the students, the girls mostly, had named about fifty or sixty, some of which the professor had never heard of. Thus I discovered where many of the girls had been spending their free afternoons. Note 2 That's my main story for this entry, and if you're not at all into math, you may want to stop reading here, and scroll to the footer to decide what to do next. If you continue reading, you'll learn how that evening, being a mathematically-oriented MIT student, I proceeded to compute the optimal place to leave the bicycle, given my walking and cycling rates, and Diane's. This was of course more an interesting mathematical exercise than anything of practical value. I'm someone who invents and solves math problems for my own amusement. I find it relaxing. As I worked through the algebra, it quickly became clear that rather than working with our walking and riding speeds, the formulas became simpler if I thought in terms of their reciprocals. That is, rather than working in terms of kilometers per hour, it was better to turn these values over, and think in terms of hours per kilometer (or even better, minutes per kilometer). For instance, if I walk at about 4 km/hr, that corresponded to 1/4 of an hour per kilometer. Multiplying by 60 minutes/hr, that's 15 minutes/km.
In electrical engineering, some components have an electrical property called "resistance", which is given in "ohms" (named after Georg Simon Ohm, a German physicist). But the reciprocal of resistance does have a name - "conductance". And when I was a student, it was measured, with a bit of engineering humor, in "mhos". That is, the unit used is the resistance unit, the "ohm", with its spelling reversed to "mho". Note 3 If you know of any word in English, or any other language, that represents the reciprocal of "speed", I'd love to hear about it. I don't think that "slowth" will catch on. Anyway, below I'll develop the formula I came up with. Looking at our trip to the Place Clemenceau: 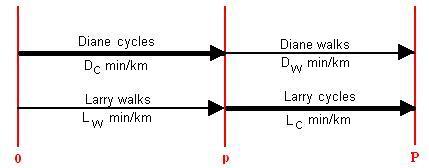 I've defined DW and DC as "Diane's walking and cycling slowth, respectively", and similarly LW and LC are defined for Larry, all units in, say, minutes per kilometer. The final distance to the Place Clemenceau is defined as P kilometers, so I used a lower-case p for the intermediate stopping point. Diane cycles the distance p first, and walks the distance (P-p) second. Larry walks p first and cycles (P-p) second. The time taken is slowth times distance (more commonly thought of as distance divided by rate). So for Larry and Diane to arrive at the same time (absent the patisserie effect): If you remember your algebra, you can then show that p/P equals: And that's what I called "the Ayache formula", in honor of Diane. For example: suppose Diane and I both walk at a speed of 4 km/hr, meaning a "slowth" of 15 minutes/km, and we both cycle at three times that speed, that is taking only 5 minutes/km. Then we should leave the bicycle the following fraction of the way to the final destination: In fact, if our walking rates are equal, and our cycling rates are equal, a glance at the formula shows that it will yield a value of 1/2 no matter what those rates are. That seemed obvious to me before I had worked through the math. If our walking rates are the same, and our cycling rates are the same, and we each cycle half the distance and walk half the distance, we're going to arrive at the same time. But suppose that although we both walk at 15 minutes/km, Diane proves to be a speed demon on the cycle, taking only 3 minutes/km, while I'm a slowpoke at 6 minutes/km. Then the formula gives That is, we should pick a point to leave the bicycle that's only about 43 percent of the way to the final destination, instead of half way. Since Diane is a faster cycler, for us both to arrive at the same time, she has to cycle less and walk more. But damn that patisserie effect!   Note 1: On November 10, 2007, it was announced in the on-line publication Altern@tives P@loises that the name of the Place Georges Clemenceau was being changed to the Place André Labarrère. This was followed by a series of comments, some quite irate, in the commentary section attached to the web page. Five days later, a posting noted that the Municipal Council, having received many complaints, had withdrawn the name change. A resident of Pau is "palois". The names of city residents are often irregular, in English as well as French. The residents of both Cambridge, England and Cambridge, Massachusetts (USA) are "Cantabrigians". I once explained to a Frenchman that while the residents of New York are "New Yorkers", the residents of Boston are "Bostonians". Then, to see if he knew "Chicagoan", I asked if he knew what the residents of Chicago are called. "Ah, Oui", he replied, "gangsters" (which he pronounced "gong-stair"). He'd evidently seen a lot of American movies. [return to text] Note 2: The French pastry name favored by adolescent students the world over is "pet de nonne" (sometimes hyphenated as "pet-de-nonne"). The name of this light beignet soufflé translates as "nun's fart". [return to text] Note 3: Because the pronunciation of the word "ohm" has the same sound as the name of the Greek letter omega (Ω), that letter has generally been used as an abbreviation for the unit. With the same engineering humor that named the unit for the reciprocal by reversing the letters of "ohm" to "mho", the unit for conductance is abbreviated with the Greek letter omega written upside-down (ʊ). After all, a value x can be thought of x/1, and hence its reciprocal, 1/x, is "upside-down". But in 1971, it was decided to rename the unit of conductance the "siemens", after the German inventor Ernst Werner von Siemens. I'm an old-timer, and I still use the "mho", myself. [return to text]  |
During my French study summer in Pau, France, in 1961, I found myself one afternoon in the company of one of the girls in our group, Diane Ayache. To the left, you can see the only picture I can find of Diane, which I scanned from a slide (I didn't take many pictures that summer). I'm sorry that it's rather out of
focus. 
To do that, I consulted my map of the city of Pau, and picked a point along our route that seemed to be half way to the Place Clemenceau. We agreed that Diane would ride the bicycle to that point, lock it up at an agreed-upon corner, and walk the rest of the way. I would walk to that point, pick up the bicycle, and ride the second half. We should both arrive at our destination at about the same time.
A linguistic digression: it seems odd to me that there is no English word for the entity that is represented in these units. There are many words describing how fast one is going: "speed", "rate", and "velocity", for instance. These can all be expressed in units such as kilometers per hour ("km/hr"), or in the United States, miles per hour ("MPH"). But although web searches indicate that some runners in the United States specify their pace in minutes per mile, what is the name of what they are specifying? It's not their speed - that would be in miles per minute, not minutes per mile. If "speed" tells how fast you're going, perhaps we can coin the word "slowth", to tell how slowly you're going (as you go more slowly, the "minutes/mile" number increases). The snail shown in the picture might have a slowth best measured in units of hours/kilometer.