If you absorbed my earlier blog entry Eleven, you can see at a glance that 1485 is indeed divisible by 11. This blog entry is about divisibility, and I'll be curious to see if anyone reads it. People who are mathematically oriented already know the divisibility tricks it explains, and people who are not mathematically oriented will probably skip this entry altogether. Although I'd suggest you don't skip it - it's really simple, and might help you understand a bit how simple math can be entertaining.

In High School, I was a member of my school's math team: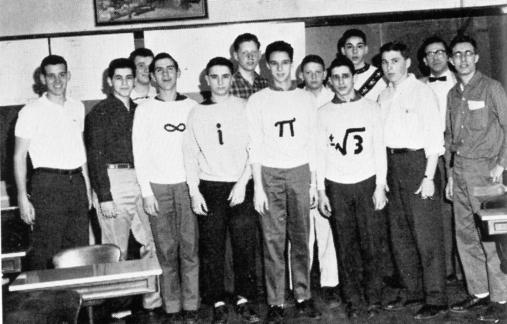

That's me in the front row, third from the right, wearing the sweatshirt showing ± the square root of three. The joke sweatshirts were sewn for the team by my mother, Rose Krakauer. ^Note 1 

In our competitions, we would be given mathematical problems, and 5 minutes to come up with an answer. A favored sort of problem turned out to be what are called "divisibility problems". That is, solving them in a short amount of time involved quickly recognizing whether or not a number was divisible by another number ("divisible" means "evenly divisible" - that is, divisible with no remainder). In particular, we were once given a substantial list of numbers, and asked to determine how many of them were divisible by 11. I didn't know how to do it at the time, but I know now.

When I use the word "number" in this entry, I actually mean an "integer", to be more exact. An "integer" is a "whole number", that is, a number without a fractional or decimal part.

Different numbers have different divisibility tricks. Here are a few of them. NOTE:  mathematicians abbreviate the phrase "if and only if" as "iff". ^Note 2

One: All numbers are divisible by 1. Duh.

Two: A number is divisible by 2 iff its last digit is even. Saying that a number is "divisible by 2" is the same as saying the number is "even". I think everyone knows that you can tell if a number is even by looking only at its last digit.

Three: A number is divisible by 3 iff the sum of its digits is divisible by 3.

Four: A number is divisible by 4 iff its last TWO digits are divisible by 4. Are you seeing a trend here? A number is divisible by 8 iff its last THREE digits are divisible by 8, divisible by 16 iff its last FOUR digits are divisible by 16, and so on. In general, A number is divisible by 2^N iff its last N digits are divisible by 2^N.

Five: A number is divisible by 5 iff its last digit is a 0 or a 5. I think everyone knows that one.

Six: A number is divisible by 6 iff it's divisible by both 2 and 3 (which see above). This is because 6 = 2 X 3.

Seven: There's no really good trick to determine divisibility by 7. There are a few pretty complicated tests, but it's really easier to just divide (especially if you have a calculator).

Eight: A number is divisible by 8 iff its last THREE digits are divisible by 8. See "four" above.

Nine: A number is divisible by 9 iff the sum of its digits is divisible by 9. This "sum of the digits" trick only works for 3 and 9.

Ten: A number is divisible by 10 iff its last digit is a 0. As with Five above, I think everyone knows that one too.

Eleven: See the picture just below. A number is divisible by 11 iff the sum of the digits in odd positions in the number and the sum of its even position digits are the same, or differ by a multiple of 11. That's why it's obvious that the number 1485, with which I opened this entry, is divisible by 11:

If I recall correctly, my Senior year in High School was the first time that Great Neck North Senior High School fielded a team in the Nassau County Mathletes. Our team didn't do all that well, because schools that had competed in previous years were more familiar with the types of problems they presented. I think our school did very much better the following year.

In the contests, we were given five minutes each to solve five problems. We were required to circle the answer on our papers, and turn them in at the end. Your work was not considered, only the circled answer, which was either right or wrong.

I don't know the history of this competition over the 55 years that have elapsed since then, but a web search turned up two current competitions, the Nassau County Junior Mathematics League and the Nassau County Interscholastic Mathematics League (the "NCIML"). As I post this entry, the latter web page notes, "Congratulations to everyone earning perfect scores on Contest #4!", and the list of names includes "Tanny Libman from Great Neck North", evidently one of my successors (who clearly had greater success than I did!).

Contests in the NCIML are divided into "Calculator" and "Non Calculator" divisions, and if you're interested, you can see the problem sets used in the competitions that have already taken place. The Junior Mathematics League seems to be for younger students, grades 7-9, and also includes high scorers from Great Neck North.

The first part of a two-part question on the first problem set of the Non Calculator contest held on October 22, 2013 was a divisibility problem. It was:

You can solve it using the divisibility tricks given above. You may want to think about it yourself, or take a look at my solution in Note 3.

Here's a brief discussion of the numbers twelve through twenty-five (or you can skip this part). There aren't many divisibility tricks for these numbers. The rules for the composite (non-prime) numbers are like the rule for Six: they have to be divisible by the powers of all their prime factors. In general, there are no good tricks for the prime numbers. Thus:

    Twelve:  Divisible by 12 iff divisible by 3 and 4.
    Thirteen:  Prime, no simple trick.
    Fourteen:  Divisible by 14 iff divisible by 2 and 7.
    Fifteen:  Divisible by 15 iff divisible by 3 and 5.
    Sixteen:  Divisible by 16 iff last 4 digits divisible by 16.
    Seventeen:  Prime, no simple trick.
    Eighteen:  Divisible by 18 iff divisible by 2 and 9.
    Nineteen:  Prime, no simple trick.
    Twenty:  Divisible by 20 iff divisible by 4 and 5.
    Twenty-one:  Divisible by 21 iff divisible by 3 and 7.
    Twenty-two:  Divisible by 22 iff divisible by 2 and 11.
    Twenty-three:  Prime, no simple trick.
    Twenty-four:  Divisible by 24 iff divisible by 3 and 8.
    Twenty-five:  Divisible by 25 iff last 2 digits divisible by 25.

And so on.

I hope you're now on better terms with some of the numbers we've discussed. But neither you nor I will ever be as close to numbers as the famous mathematician Srinivasa Ramanujan. In a famous story about Ramanujan told by British mathematician G. H. Hardy:

The mathematician J. E. Littlewood, upon hearing of the taxicab incident, noted, "Every positive integer is one of Ramanujan's personal friends." ^Note 4

Margie wants to know why any of this matters. I think it's fun.

Extra credit: is "divisibility" the only word in English with five i's in alternating positions? I haven't got the faintest idea. I think that "bookkeeper" is the only English word with three double letters in a row.
 

Note 1:   The picture was scanned from the 1959 Arista, the Great Neck North High School yearbook. The other members of the team are identified under the photo as: Front row, left-to-right: E. Gruenstein, D. Levy, C. Bender, D. Bloch, R. Ott, L. Krakauer, K. Post, and R. Sylvan. Second row, left-to-right: R. Gruen, M. Schoenberg, P. Spiegelman, S. Einhorn, and the faculty adviser Mr. Isaacs.

This picture and a bit of the associated text were taken from my entry Eleven.   [return to text]

Note 2:   There are obviously 26³ = 17,576 ordered triplets of three letters. Combinations that use common letters often turn out to be abbreviations for multiple things in English. An interesting way to find out what an abbreviation might mean is to search for it on Wikipedia. For example, if you do a search on "IFF", you can get to a page like http://en.wikipedia.org/wiki/IFF_(disambiguation) which lists a whole lot of possible meanings. In addition to "if and only if", the military transponder "Identification Friend or Foe" was the other meaning that came to my mind.  [return to text]

Note 3:   The problem:  "What is the largest three-digit number divisible by 3, 4, 5, and 6?"  The divisibility tricks given above in this entry are all you need to reason your way to an answer in a matter of seconds - the spelled-out numbers in boldface below refer to the rules given above.

Since the number must be divisible by Five it must end in a 5 or a 0, but since it must also be divisible by Four, it must be even, and hence must end in a 0.

Then, to be divisible by Four its last two digits must be divisible by 4, so to also end in a 0, it must end in 00, 20, 40, 60, or 80. To get the highest possible three-digit number, can we put a 9 in front of any of these to get a three-digit number divisible by 3? Which of the following are divisible by Three: 900, 920, 940, 960, 980?

Since the first digit, the 9, is itself divisible by three, it doesn't change the divisibility by 3 of the sum of the digits. And since the last digit is 0, it doesn't count either, meaning that the only remaining (center) digit must be divisible by 3. Only 0 and 6 meet that requirement, so 900 and 960 are the only two numbers in the 900's that are divisible by 3, 4, and 5. Obviously, 960 is the larger of the two, and that is the answer.

You might note that nowhere in my reasoning did I consider that the answer had to also be divisible by Six, as specified in the problem. That's because if a number is divisible by 4, it has to also be divisible by 2, and a number that's divisible by both 2 and 3 must also be divisible by 6. Hence that part of the specification is irrelevant. If a number is divisible by 3 and 4, it will automatically be divisible by 6. A common way to make mathematical problems a bit more difficult is to include irrelevant information in the problem statement.   [return to text]

Note 4:   All these notes about Ramanujan, including citations for the Ramanujan and Littlewood quotes, can be found in the Wikipedia article on the number 1729. The two ways in which 1729 can be expressed as the sum of two cubes are 1729 = 1³ + 12³ and 1729 = 9³ + 10³. As Ramanujan knew off the top of his head (although it's hardly obvious), no number smaller than 1729 can be expressed as the sum of two cubes in more than one way.  [return to text]